(Syllabus) CBSE Syllabus of Mathematics for Class 12 | March 2009 Examination

Disclaimer: This website is NOT associated with CBSE, for official website of CBSE visit - www.cbse.gov.in

Syllabus : CBSE Syllabus of Mathematics for Class 12 For March 2009 Examination

COURSE STRUCTURE
Class XII | Mathematics
One Paper 3 Hours 100 Marks

UNIT I. RELATIONS AND FUNCTIONS

1. Relations and Functions : (10) Periods

Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions, composite functions, inverse of a function. Binary operations.

2. Inverse Trigonometric Functions: (12) Periods

Definition, range, domain, principal value branches. Graphs of inverse trigonometric functions. Elementary properties of inverse trigonometric functions.

UNIT-II: ALGEBRA

1. Matrices: (18) Periods

Concept, notation, order, equality, types of matrices, zero matrix, transpose of a matrix, symmetric and skew symmetric matrices. Addition, multiplication and scalar multiplication of matrices, simple properties of addition, multiplication and scalar multiplication. Non-commutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Concept of elementary row and column operations. Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).

2. Determinants: (20) Periods

Determinant of a square matrix (up to 3 x 3 matrices), properties of determinants, minors, cofactors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of solutions of system of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.

UNIT-III: CALCULUS

1. Continuity and Differentiability: (18) Periods

Continuity and differentiability, derivative of composite functions, chain rule, derivatives of inverse trigonometric functions, derivative of implicit function. Concept of exponential and logarithmic functions and their derivative. Logarithmic differentiation. Derivative of functions expressed in parametric forms. Second order derivatives. Rolle's and Lagrange's Mean Value Theorems (without proof) and their geometric interpretations.

2. Applications of Derivatives: (10) Periods

Applications of derivatives: rate of change, increasing/decreasing functions, tangents & normals, approximation, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).

3. Integrals: (20) Periods

Integration as inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions and by parts, only simple integrals of the type as below to be evaluated.

${ \int {{{dx} \over {x^2  \pm a^2 }}} ,\int {{{dx} \over {\sqrt {x^2  \pm a^2 } }}} ,\int {{{dx} \over {\sqrt {x^2  - a^2 } }}} ,\int {{{dx} \over {ax^2  + bx^2  + c}},\int {{{dx} \over {\sqrt {ax^2  + bx^{}  + c} }}} }   \cr   \int {{{(px + q)} \over {ax^2  + bx^{}  + c}}dx,} \int {{{(px + q)} \over {\sqrt {ax^2  + bx^{}  + c} }}} dx,\int {\sqrt {a^2  \pm x^2 } } dx,\int {\sqrt {x^2  - a^2 } } dx \cr}$

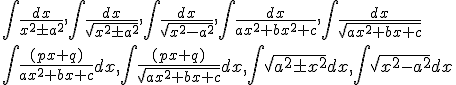
Definite integrals as a limit of a sum, Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.

4. Applications of the Integrals: (10) Periods

Applications in finding the area under simple curves, especially lines, areas of circles/ parabolas/ellipses (in standard form only), area between the two above said curves (the region should be clearly identifiable).

5. Differential Equations: (10) Periods

Definition, order and degree, general and particular solutions of a differential equation. Formation of differential equation whose general solution is given. Solution of differential equations by method of separation of variables, homogeneous differential equations of first order and first degree. Solutions of linear differential equation of the type:

${{dy} \over {dx}} + py = q$ where p and q are functions of x.

UNIT-IV: VECTORS AND THREE-DIMENSIONAL GEOMETRY

1. Vectors: (12) Periods

Vectors and scalars, magnitude and direction of a vector. Direction cosines/ratios of vectors. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Scalar (dot) product of vectors, projection of a vector on a line. Vector (cross) product of vectors.

2. Three - dimensional Geometry: (12) Periods

Direction cosines/ratios of a line joining two points. Cartesian and vector equation of a line, coplanar and skew lines, shortest distance between two lines. Cartesian and vector equation of a plane. Angle between (i) two lines, (ii) two planes. (iii) a line and a plane. Distance of a point from a plane.

UNIT-V: LINEAR PROGRAMMING

1. Linear Programming: (12) Periods

Introduction, definition of related terminology such as constraints, objective function, optimization, different types of linear programming (L.P.) problems, mathematical formulation of L.P. problems, graphical method of solution for problems in two variables, feasible and infeasible regions, feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).

UNIT-VI: PROBABILITY

1. Probability: (18) Periods

Multiplication theorem on probability. Conditional probability, independent events, total probability, Baye's theorem, Random variable and its probability distribution, mean and variance of haphazard variable. Repeated independent (Bernoulli) trials and Binomial distribution.